Learning without Labels
By Aashish Jain and Michael Sollami
“If intelligence was a cake, unsupervised learning would be the cake, supervised learning would be the icing on the cake, and reinforcement learning would be the cherry on the cake.” — Yann LeCun
In 2019, Yann LeCun revised the above quote, changing “unsupervised learning” to “self-supervised learning,” and in 2020 he declared that self-supervised learning (SSL) is the future of machine learning. Simply stated, SSL is a form of unsupervised learning where the input data generates its own labels. To accomplish this, part of the data is withheld, creating a ‘pretext’ or ‘self-supervision’ task where the model must predict the withheld data, with the loss used for supervision of the model. Examples of pretext tasks include masked word prediction, corrupted input recovery, and image patch ordering. Afterwards this ‘pre-trained model’ is finetuned for specific tasks by adding smaller networks trained on actual labels for a task. However, labeling data is an intensive process and supervised deep learning models rely on large labeled datasets - which presents a fundamental bottleneck as since humans must manually annotate data. Self-supervised learning reduces the need for labels, paving a path for cheaper, more data-efficient AI!
A Success Story in NLP
In recent years, the application of transformer models such as BERT yielded many successes in the field of NLP, showing the potential of self-supervised learning. Large web-scraped datasets combined with unsupervised tasks, like masked language modeling, results in base networks capable of generating high-quality contextualized sentence encodings. Starting from such pre-trained networks, state-of-the-art performance is then achieved in various downstream tasks (such as classification, named entity recognition, question answering, etc.) without the need for any highly task-specific architectures. As most of the learning is done during the self-supervised pre-training phase, tuned models can achieve good results even with limited labeled data.
Self-supervised learning in Computer Vision
Transfer learning of supervised models still dominates in the vision space, however, we see promising results of self-supervised image representation learning using contrastive learning. In contrastive learning, the model must distinguish between similar and dissimilar data points. By learning that, the model outputs similar representation for similar inputs.
Momentum Contrast (MoCo)
Momentum Contrast (Chen et al., 2020) frames contrastive learning as a dynamic dictionary lookup, with comparison of encoded queries to a dictionary of encoded keys using a contrastive loss function. For each image, a standard compliment of augmentation operations are performed at random (e.g. color jittering, flips, etc.). The learned representation of different augmentations of the same image should be similar.
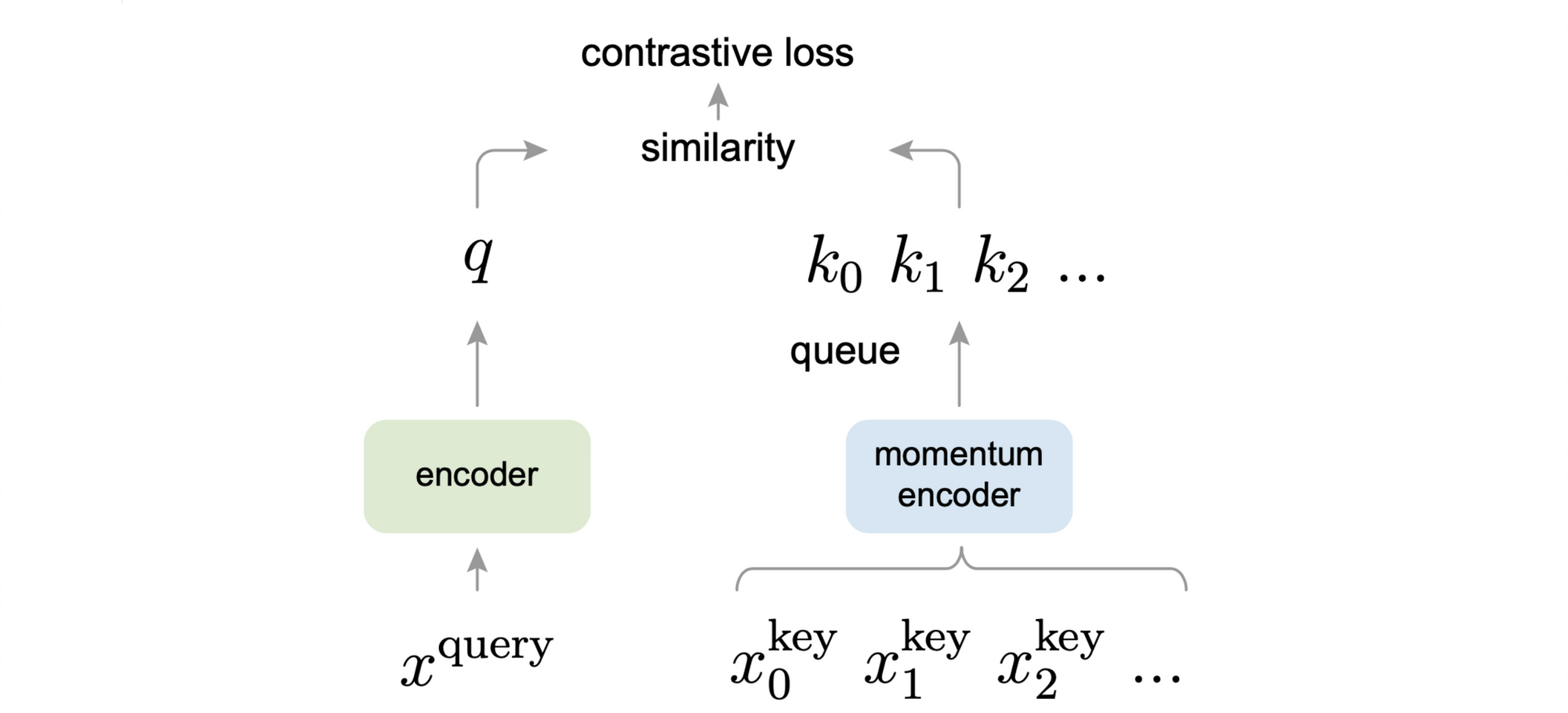
In this approach, the authors encode a query image \(x^{query}\) using an encoder \(f_q\) to \(q\), and the images in dictionary keys \(x_0^{key}, x_1^{key}, x_2^{key}\cdots\) are encoded into \(k_0, k_1, k_2\cdots\) using a separate encoder \(f_k\). A single key \(k_+\) is a different augmentation of same image as query forming a positive key. The InfoNCE contrastive loss \(\mathcal{L}_q\) is computed as
\[\mathcal{L}_q = - \log \frac{exp(q\cdot k_+/\tau)}{\sum_{i=0}^K exp(q\cdot k_i / \tau)}\]
where \(\tau\) represents the a temperature hyperparameter. This loss decreases when the similarity between \(x^{query}\) with positive keys is high and with \(K\) negative keys is low.
During training, we add the current mini-batch to the dictionary and remove the oldest mini-batch, making the size of keys independent of batch size, allowing for large key sizes. To maintain consistency of preceding mini-batches keys, the key encoder \(f_k\) slowly progresses through momentum update. Assuming parameters of \(f_k\) be \(\theta_k\) and \(f_q\) be \(\theta_q\), we define the momentum update as \(\theta_k \leftarrow m\theta_k + (1-m)\theta_q\)
where \(m\) is a momentum coefficient. Note that here the gradients only flow through \(θ_k\) during back-propagation.
Hinton's SimCLR
SimCLR (Xinlei Chen et al., 2020) presents a simpler framework for contrastive learning with the additional transformation of learned representation only for contrastive loss.
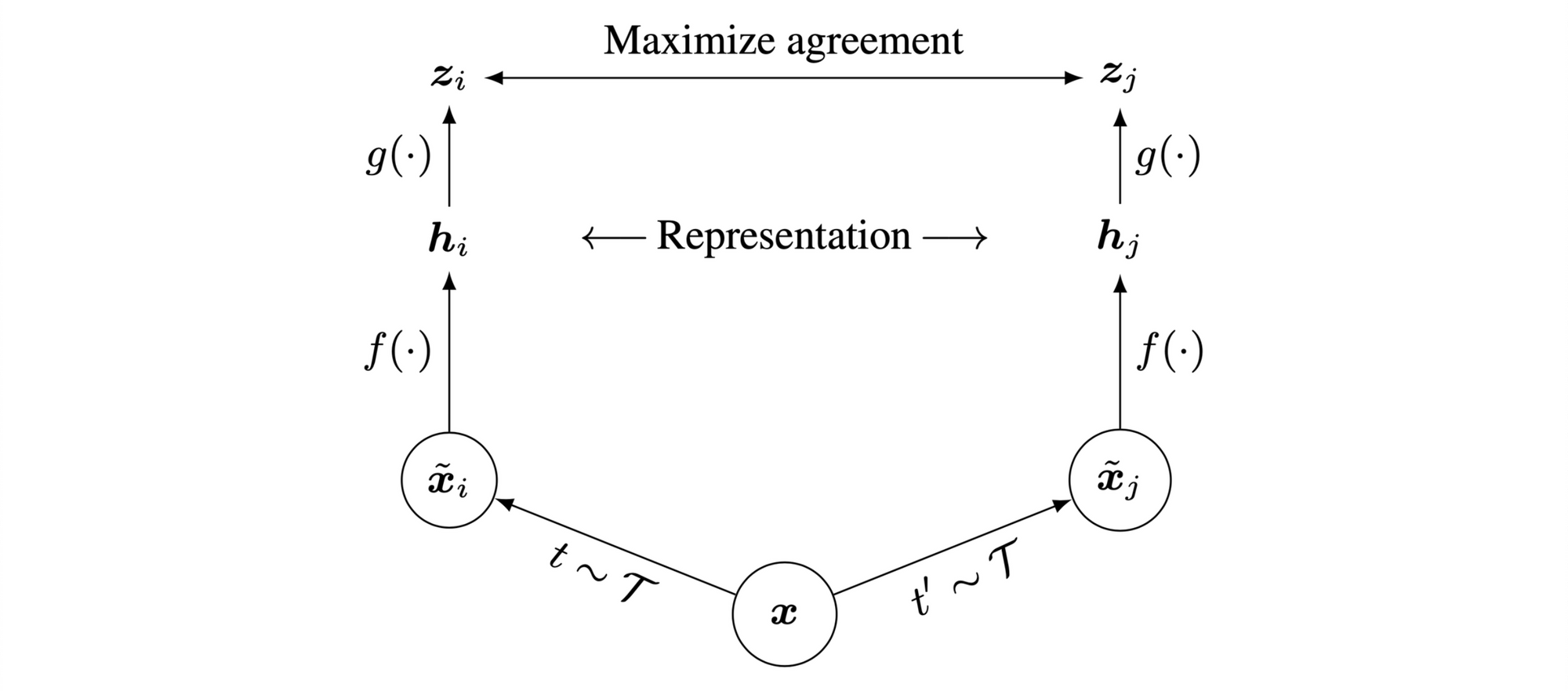
We depict the central idea of this framework in the accompanying figure. For a given image \(x\), two data augmentations \(t, t^\prime\) are sampled from \(\mathcal{T}\) and performed resulting in \(\tilde{x_i}, \tilde{x_j}\) respectively. We repeat this process for all \(n\) images in the mini-batch, resulting in a single positive pair and \(2(n-1)\) negative examples. The encoder \(f(\cdot)\) encodes the augmented sample giving a representation \(h\). A non-linear projection head \(g(\cdot)\) transforms \(h\) into \(z\) over which the contrastive loss is computed.
The two key takeaways from SimCLR are a) adding a learnable non-linear MLP projection head for contrastive loss and b) composition of strong data augmentations (which includes random cropping, color distortions, and gaussian blur) greatly improves the learned representation.
SimCLR performance depends heavily on the mini-batch size, as it controls the size of the negative sample. It was trained on mini-batch size 4096, much larger than that in traditional supervised learning. On the other hand, MoCo mitigates this dependency by maintaining dynamic dictionaries of previous mini-batch samples in combination with momentum encoder updates.
Finally, MoCoV2 combines SimCLR’s takeaways with MoCo, achieving better performance than both without the requirement of large training mini-batches. In their follow-up paper from March of this year, a few simple modifications where made. Namely, they added an MLP projection head and performed more data augmentation, which together establishes slightly stronger baselines over SimCLR.
Bootstrap Your Own Latent (BYOL)
BYOL (Grill et al., 2020) presents a new approach for representation learning without using negative examples.
BYOL consists of two networks online and target both having the same architecture. For input image \(x\) two different views \(v, v^\prime\) are generated from randomly selected augmentations \(t, t^\prime\). They are encoded using encoder \(f_\theta, f_\xi\) into image representation \(y_\theta=f_\theta(v)\) and \(y_\xi^\prime=f_\xi(v^\prime)\), which is then projected (similar to SimCLR) using projector \(g_\theta, g_\xi\) into \(z_\theta=g_\theta(y_\theta)\) and \(z_\xi^\prime = g_\xi(v^\prime)\). The online network consists of a predictor \(q_\theta\) which outputs prediction \(q_\theta(z_\theta)\). Note that \(sg\) stands for stop-gradient. The similarity loss is computed between the L2 normalized \(q_\theta(z_\theta)\) and \(z^\prime_\xi\). During training, only \(\theta\) are updated and \(\xi\) are an exponential moving average of \(\theta\) (similar approach to MoCo). After training, \(f_\theta\) is used to get the image representation.
The surprising thing about BYOL is that even without negative examples the model does not collapse to constant representation for all images. The authors hypothesize that is because the target parameters \(\xi\) updates are based on \(\theta\) and not in the direction of \(\nabla_\xi\) of BYOL loss function \(L_{\theta, \xi}^{BYOL}\), the gradient descent would not converge to the minimum of \(L_{\theta, \xi}^{BYOL}\) with respect to both \(\theta\) and \(\xi\), thus preventing constant collapsed representation.
How does it perform?
The semi-supervised evaluation involves fine tuning the pretrained network with MLP classification head, using fewer labels. With only 1% labeled dataset and ResNet-50(4x) encoder, SimCLR and BYOL achieves 63.0% and 69.1% accuracy respectively on ImageNet. When provided 10% of the labeled dataset, the performance increases to 74.4% (SimCLR) and 75.7% (BYOL), compared to 78.9% accuracy of baseline fully supervised network. These are encouraging results, showing that self-supervised learning makes the models significantly more data efficient.
Enter DINO
In a recent paper Facebook researchers explored self-supervised pretraining on vision transformer (ViT) features (Caron et al., 2021). Their result is a system called DINO, which stands for self-distillation with no labels, and achieves 80.1% top-1 on ImageNet in linear evaluation with ViT-Base. The loss used in DINO is a cross-entropy on softmax sharpened outputs, unlike MoCo-v2 which uses contrastive loss, and BYOL, which uses mean squared error. The DINO approach demonstrates the importance of using smaller image patches with ViT's while hitting upon a clever way of doing distillation - while training the student and teacher networks, their teacher is updated with an exponential moving average of the student. The features of DINO are shown to have enable high downstream performance with regard to semantic representation and low-shot learning tasks. This is a nice result, and there is much more to be done along these lines!
What’s in the Future?
Self-supervision not only presents solutions for tasks where labels are limited - a practical advantage which helps make SSL a very active research area - but unlocks potential solutions in areas where supervision and reinforcement fail. In the near future, we foresee self-supervised image and video representation models pre-trained on vast amounts of unlabeled data. Utilizing such representations will lead to more data efficient downstream models for computer vision tasks and aid in active learning, where self-supervised loss can determine the importance of labeled examples.