TLDR

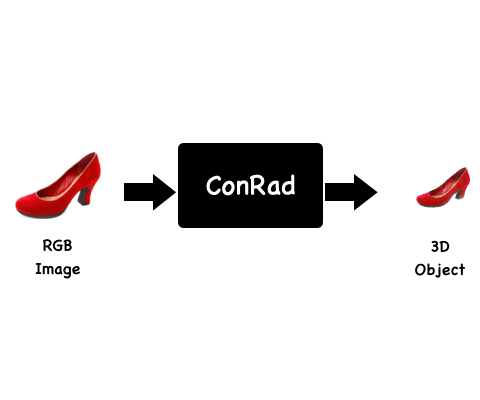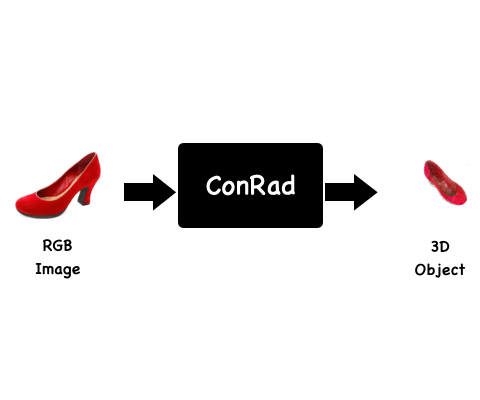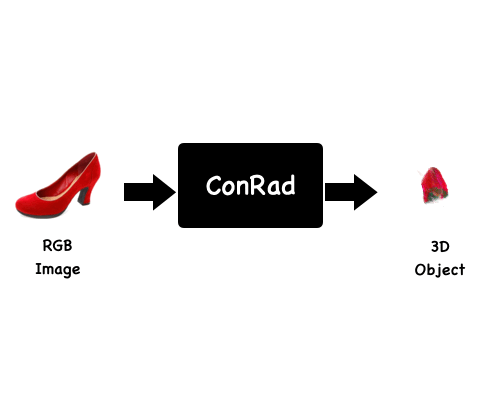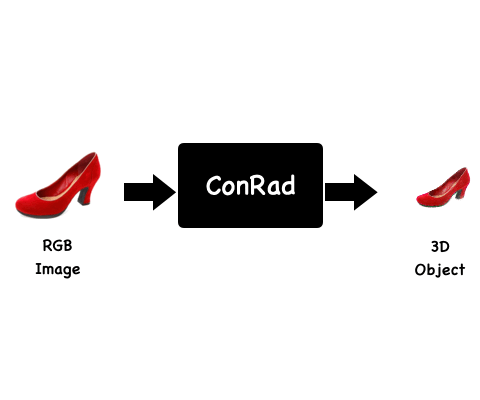
We present ConRad, a novel approach for generating a 3D model from a single RGB image. We introduce a 3D representation that allows us to explicitly constrain the appearance of the object using the input image which leads to preservation of depicted details.  

Background

Over the last few years, approaches for generative modeling in Computer Vision have demonstrated tremendous success. We now have incredibly mature approaches for synthesizing images with user-desired content, editing images based on human instructions, personalized image generation, etc. At the core of many of these methods is the idea of diffusion models¹. These models generate images by starting with a completely noisy image and progressively de-noising it. Here you can see results from a popular text-to-image generation model (Stable Diffusion²) and a recent image editing approach (EDICT³).

While these approaches are able to generate high-quality images, they are restricted to producing 2D images and do not provide a means to generate 3D models. However, in our real world, we rarely deal with 2D images - we interact with 3D objects, we infer the 3D structure of objects around us and we plan our actions based on the 3D structure of the world. As we make progress towards providing richer virtual experiences, the ability to generate and interact with 3D data becomes increasingly important. For example, being shown an image of a sofa and showing how it looks in your living room in 3D provide vastly different shopping experiences.

Inspired by this, over the last few months, researchers have developed approaches to generate 3D models from user provided text prompts. DreamFusion⁴ is one such approach that can generate 3D models by leveraging pre-trained 2d image diffusion models. Similar to how images are represented as a 2D grid of pixels, 3D models are represented as a 3D grid of voxels where each location stores the density and color^*. Looking at a 3D model  from a specific viewpoint (rendering)  gives us a 2D image of it. DreamFusion works on the key idea that progressively de-noising these images of all the viewpoints using a diffusion model could lead to a consistent 3D model of the desired object. This approach of "distilling" the knowledge of a diffusion model into a 3D representation is called Score Distillation Sampling.

[*] In practice, most approaches implement the 3D grids as a continuous radiance field. This blog attempts to simplify concepts to make it more accessible.

Problem

DreamFusion⁴ and many followup works^5,6 have demonstrated the ability to generate 3D from text prompts. However, these approaches do not provide a straightforward way to generate a 3D model of a given input image. The ability to generate 3D models of a given object image has numerous applications - in e-commerce for providing a richer shopping experience,  in AR/VR and video-games for asset generation from images, in marketing for animation and even in more complex domains like robotics for reasoning about interactions with objects.

In this work, we address this problem of generating a 3D model from a given input image of an object. The goal is to generate a 3D model that remains faithful to the input object in both appearance and semantics i.e. it should be a realistic 3D reconstruction of the same instance of the object.

Results

First we begin by presenting some results on converting images to 3D models using our proposed approach.

Our approach also provides the capability of generating 3D models from text prompts by first generating an image text --> image using Stable Diffusion and then lifting the image to a 3D model image --> 3D using our approach.

In recent concurrent research, RealFusion⁷ and NeuralLift360⁸ are two solutions to the same problem. In contrast to our approach, these methods rely on applying additional loss functions to constrain the 3D representation to match the input image. Since these methods rely on multiple objectives it often leads to a trade-off between matching the input image and generating an arbitrary 3D object of the same category. We show here our approach produces 3D models that are more faithful to the input image in more viewpoints.

Please refer to the upcoming paper for more results.

Solution: ImageDetail3D

In this section, we present a high-level overview of our approach. In order to generate a 3D model of the object, we propose to optimize a 3D representation similar to DreamFusion (imagine a 3D grid of voxels). This representation is initially a blob of density in the center of the grid that doesn't look very meaningful from any viewpoint:

For a user provided image (like this shoe below), we want the final 3D representation to look like this shoe in one viewpoint and look like a realistic rotation of this shoe in the other viewpoints.

First, we propose a novel approach to constrain the rendering of the 3D representation in one viewpoint to exactly match the input image regardless of the distribution of density in the 3D grid. Here we show the renderings of the initial 3D representation after applying our constraint algorithm.

As you can see, while the input matches in one viewpoint, it looks meaningless in all the other viewpoints. In order to make the other viewpoints look realistic and cohesive, we need to de-noise the density and color of the 3D voxel grid. This can be accomplished by distilling knowledge from a diffusion model similar to DreamFusion. We perform the following steps iteratively:

1. Randomly sample a viewpoint
2. Render the 3D representation from this viewpoint
3. Update the 3D representation using Score Distillation Sampling (proposed in DreamFusion)

After updating the 3D representation for many iterations, we end up with a 3D model that looks like this:

Note: this summary presents a simple explanation of our approach. All the details with additional constraints and regularizations will be available in the full paper.

Deeper Dive - Image Constrained 3D Representation

In this section, we present some more details of the formulation of our 3D representation that allows us to preserve details depicted in the input image. We implement our 3D representation as a radiance field \( \mathcal{F}_\theta : (x) \xrightarrow{} (c, \sigma) \) that maps a point in 3D \( x \) to a color \( c \) and density \( \sigma \). Rendering the 2D image of a viewpoint of the radiance field can be achieved by accumulating color over points sampled on camera rays. For a camera ray \(\textbf{r}(t) = \textbf{o} + t \textbf{d} \), the accumulated color is normally expressed as:
\[ C(\textbf{r})= \int_{t_n}^{t_f} T(t) \sigma(t) c(t) dt \]

where \( T(t) = exp(-\int_{t_n}^{t} \sigma(s) ds) \) is the accumulated transmittance of the volume along the ray.

We modify this expression to incorporate our input image as a constraint on the radiance field. Let \( T_{ref} \) be the projection from world coordinates to the image coordinates for the viewpoint of the input reference image. Under some assumptions on the object properties, we can make inferences about the 3D space around this object. Any point that lies behind the visible surface of this shoe is unknown and needs to be inferred in our radiance field. Any point that lies on/in front of the visible surface is known to us and does not need to be re-inferred in our radiance field i.e. points \( x \) in front of the surface have (zero density, arbitrary color) and points \( x \) on the surface have (high density, color of \( T_{ref} (x) \) ).  

These constraints are easy to incorporate if we also knew the depth values of each pixel in the reference image. For now, let the depth of \( T_{ref} (x) \) be known as \( d_{ref} (x) \). We can reformulate the radiance field as:

\[ F_{constrained}(x) = \begin{cases} (\ 0, I(T_{ref}(x))\ )   , & \text{if}\ T_{ref}(x) < d_{ref}(x) - \delta \\ (\ \lambda, I(T_{ref}(x))\ ) , & \text{if}\ |T_{ref}(x) < d_{ref}(x)| < \delta  \\ F_\theta(x) , & \text{otherwise} \end{cases} \]

where \( \lambda \) is a large density value and \( \delta \) is a hyperparameter to allow some variance in the depth of the surface.  

In practice, since we are only given an image as input, the depth value \( d_{ref} (x) \) is unknown. We overcome this challenge by relying on the current state of the radiance field to infer \( d_{ref} (x) \) by solving \( \frac{T(t)}{T(t_n) - T(t_f)} = 0.05 \) for the camera ray corresponding to \( T_{ref}(x) \). The motivation for this heuristic is to find a point along the ray beyond which the transmittance is very low.  Using these estimates, we reformulate the constraints as:

\[ F_{constrained}(x) = \begin{cases} (\ \sigma(x), I(T_{ref}(x))  \ )   , & \text{if}\ T_{ref}(x) < d_{ref}(x) + \delta \\ F_\theta(x) , & \text{otherwise} \end{cases} \]

Intuitively, during the optimization, the density estimates in the radiance field control the location and contour of the surface but the color is projected directly from the image.

Impact and Ethical Considerations

The ability to generate 3D models opens up new avenues of control over the generation process. While several text to 3D models have been proposed, their controllability is limited, which in turn limits the potential applications. The ability to control 3D generation through input images opens up novel applications. These models can improve efficiency in creation of games, marketing videos and enable creative domains like 3D art. The generation of 3D models can also significantly improve the richness of our interactions with the virtual world. Most e-commerce websites still rely on 2D photographs because scanning 3D objects is not scalable. The ability to interact with automatically generated 3D objects and observe them in AR/VR could significantly enhance the online shopping experience.

As with most generative modeling methods, it is important to be mindful of several ethical considerations. Diffusion models are susceptible to modeling harmful biases from training data including under-representation of certain races or cultures. The lack of strong filtering of the training data for the diffusion models could lead to learning of inappropriate/NSFW content. While our method does not involve training on additional data, it heavily relies on pre-trained diffusion models and could potentially regurgitate some of these biases.

Conclusion and Future

In summary, we present an approach that can build a 3D model from a single input image. The proposed method leverages a novel radiance field that allows matching an image on a single viewpoint while still allowing optimizability for other viewpoints. This blog does not cover the failure cases of our approach which will be included in the paper. Future work in this domain could focus on improving the resolution of 3D models, methods for avoiding "floaters" visible in the above results and exploring beyond single object images to full scene images.

References:

1. Kingma, Diederik, et al. "Variational diffusion models." Advances in neural information processing systems 34 (2021): 21696-21707.
2. Rombach, Robin, et al. "High-resolution image synthesis with latent diffusion models." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022.
3. Wallace, Bram, Akash Gokul, and Nikhil Naik. "EDICT: Exact Diffusion Inversion via Coupled Transformations." arXiv preprint arXiv:2211.12446 (2022).
4. Poole, B., Jain, A., Barron, J. T., & Mildenhall, B. (2022). Dreamfusion: Text-to-3d using 2d diffusion. arXiv preprint arXiv:2209.14988.
5. Lin, Chen-Hsuan, et al. "Magic3D: High-Resolution Text-to-3D Content Creation." arXiv preprint arXiv:2211.10440 (2022).
6. Chen, Rui, et al. "Fantasia3D: Disentangling Geometry and Appearance for High-quality Text-to-3D Content Creation." arXiv preprint arXiv:2303.13873 (2023).
7. Melas-Kyriazi, Luke, et al. "RealFusion: 360 {\deg} Reconstruction of Any Object from a Single Image." arXiv preprint arXiv:2302.10663 (2023).
8. Xu, Dejia, et al. "NeuralLift-360: Lifting An In-the-wild 2D Photo to A 3D Object with 360° Views." arXiv e-prints (2022): arXiv-2211.

About the authors

Senthil Purushwalkam is a Research Scientist at Salesforce AI. His research interests like in Computer Vision and Machine Learning.

Nikhil Naik is a Principal Researcher at Salesforce AI.